Hur fungerar binära tal?

Du kanske hört talas om binära tal, men vad är de egentligen?
Det talsystem vi använder i större delen av världen idag är det decimala talsystemet som är baserat på 10-potenser (tio, hundra, tusen osv), och som har 10 olika “lägen” (0-9).
Det binära talsystemet däremot, som representerar tal i tvåpotenser som har två möjliga lägen (0, 1), har blivit en aning bortglömt. Men! Datorer använder sig av det för att representera all data. Du kanske hört begreppet “ettor och nollor”, och det är precis det det handlar om.
När man ska lagra ett tal binärt i en dator, måste man först bestämma hur många bitar man vill använda. En “bit” är antingen etta eller nolla.
Låt oss säga, för ett enkelt exempels skull, att vi lagrar heltal som är fyra bitar.
Då skulle talet “0” se ut som följer (raden under kännetecknar vad varje bit representerar för heltal):
0 0 0 0
8 4 2 1

Eftersom vi har talet noll, är alla bitarna noll. Om vi nu tar talet “3”:
0 0 1 1
8 4 2 1

Här är biten för “2” och för “1” aktiva. För att läsa av talet adderar man värdena under, så i detta fall blir det 1+2. Vilket är då det största talet vi kan representera med 4 bitar?
1 1 1 1
8+4+2+1 = 15

Svaret är, som synes, 15!
En liten anekdot på det; den som spelat “Final Fantasy” kanske kommer ihåg att i de tidigare spelen var det högsta värdet man kunde få på ett attribut “255”. Detta är en kvarleva från NES-eran, då man bara kunde lagra 8 bit stora tal.
Och det största talet på 8 bitar: 1+2+4+8+16+32+64+128 = 255

Nu när vi vet hur binära tal är uppbyggda kan vi också titta lite kort på hur man räknar med dem! Varför då, frågar du?
Jo, att räkna binärt är lite bökigt för den ovane, men det är väldigt enkelt att bryta ner beräkningarna i väldigt enkla metoder vilket jag kommer visa!

Addition

Om man ställer upp två binära tal på varsin rad kan man hyfsat enkelt addera dem (här i exemplet adderar jag 3 + 6):

0 0 1 1 = 3
0 1 1 0 = 6
=======
0 1 2 1
0 2 0 1
1 0 0 1 = 9

Tvåor finns ju egentligen inte i det binära talsystemet, men anledningen till att jag använder dem här är för att illustrera att vi har två bitar på samma position. Då flyttas biten nämligen fram ett steg, eftersom talet är dubbelt så stort.

Subtraktion

I fallet med subtraktion är det snäppet klurigare. Men man får börja med alla bitar där båda talen har “etta” på respektive bit och sätta noll.
Därefter finns det två olika fall, enkla att illustrera.
Det första exemplet:
1 0
0 1
===
0 1

Vi har ett tal minus ett hälften så stort tal. Svaret blir såklart, samma som det hälften så stora talet.
Och så det andra exemplet:

1 0 0
0 0 1
=====
0 1 1

Ett betydligt större tal minus ett mindre. Hur stort talet är spelar ingen roll, det enda man behöver göra är inversera de berörda bitarna i det första talet för att få fram svaret.

Var i bitsekvensen dessa mönster återfinns spelar ingen roll, så därför kan jag visa detta med två beräkningar, varav den första 14-9:

1110 = 14
1001 = 9
#====>  (plockar bort största biten, samma på båda)
0110
0001
#====> (det enkla fallet på de två minsta bitarna)
0101 = 5

För att illustrera det andra fallet, beräknar vi 16-1:

10000 = 16
00001 = 1
#====> Ta bort största biten, inversera övriga
01111 = 15

Multiplikation och division

De tidigare nämnda räknesätten kan kanske vara praktiska vid stora beräkningar (men antagligen inte).

Det binära talsystemet är däremot väldigt praktiskt när man multiplicerar och dividerar!

Vid multiplikation ställer man upp två led, ett under det ena talet och ett under det andra man ska multiplicera. Därefter skriver man det binära talsystemet under det första talet, men bara så många av talen man behöver för att representera talet. Under det andra talet skriver man först samma tal, och därefter dubblar man det tills man har lika många rader som i första kolumnen. Så här skulle det kunna se ut:

Sen då? Jo, under det första talet markerar man de tal som krävs för att representera talet 18, det vill säga 16 och 2. Sedan adderar man de tal som står på samma rader för det andra talet, i det här fallet 68 och 544:

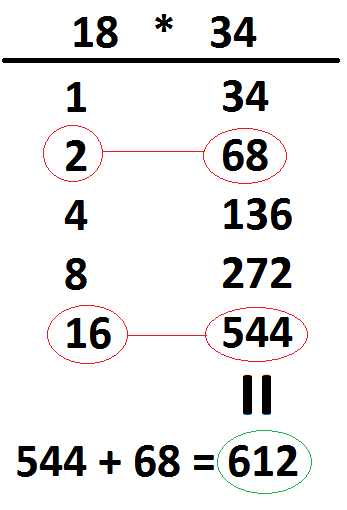
Dags för kontrollräkning med miniräknare! 😉

Att dividera fungerar ungefär likadant, fast bakvänt. Observera att det då bara fungerar när man inte får en rest. Kommer inte gå in i detalj på hur det fungerar, utan kan istället rekommendera Youtube-videon nedan!

 

https://www.youtube.com/watch?v=Ih1ZWE3pe9o

Det var allt för denna gång, hoppas det har varit någorlunda lärorikt! 🙂